Parallelisable Memory Recurrent Units

Florent De Geeter, Gaspard Lambrechts, Damien Ernst and Guillaume Drion

Link: https://hdl.handle.net/2268/339817

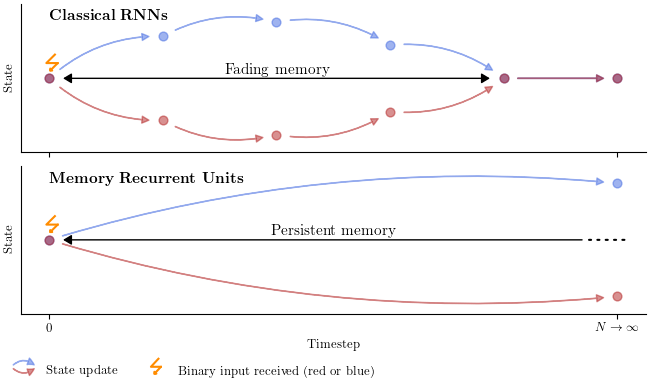
Sequence models are important because they are used everywhere: to predict future weather, to take future actions from past observations in reinforcement learning, or even to generate the following words in a sentence given past words, as is, for example, ChatGPT doing. An architecture has reigned as king for many of those tasks over the last decade, the Transformer (Vaswani et al., 2017). This architecture, though super effective at training, implements an ineffective generative process: for any word to generate, it processes all previous words again. It contrasts with the good old recurrent neural networks (RNN) that update their memory at each generated word, so as to predict the next word based on that only. Unfortunately, this sequential update has been preventing from training RNNs on large amounts of long sequences of texts. This explains the rapid adoption of Transformers, that are able to process the sequence in parallel on GPU. Recently, a new RNN has made its apparition, the state space model (Gu et al., 2021). Because of its simplified recurrence, or memory update, it can be trained by attending the whole sequence in parallel on GPU. And because it is an RNN, it has this nice, convenient, memory update that does not require to read every previous word again when generating a new word. However, as mentioned above, it is parallelisable because its recurrence is simple, so simple that it is impossible for it to keep memory over an extended period of time. Our previous works (Vecoven et al., 2021; Lambrechts et al., 2023) showed that multistable RNNs palliate this problem of fading memory. However, such RNNs cannot be parallelised like SSMs. Our recent paper (De Geeter et al., 2026) introduces a new concept of RNNs, called the Memory Recurrent Unit (MRU) that achieves persistent memory thanks to multistability while maintaining the ability to process the sequence in parallel over a GPU.

Convergent RNNs

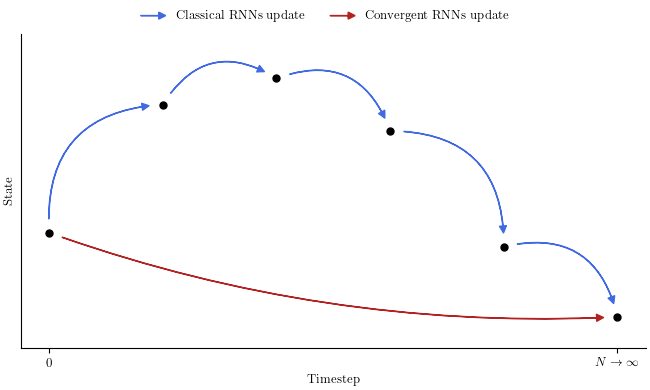
Classical RNNs can be seen as learnable discretised dynamical systems. They receive a input and update their state, based on their previous state and the input. Repeating this step creates a trajectory, that fluctuates over time depending on the inputs and the internal dynamics. Our approach is different. We introduce convergent RNNs: RNNs whose update step is not a single step of a dynamical system, but a full trajectory. We can rephrase it that way: Classical RNNs answer the question: what will be the next state of the underlying dynamical system ? While convergent RNNs answer the question: towards which state will the underlying dynamical system converge if I keep applying the same input for an infinite duration. Figure 1 illustrates this concept by comparing a classical and a convergent RNN. The classical one typically needs an infinite number of updates to reach the same state obtained after one update of the convergent RNN.

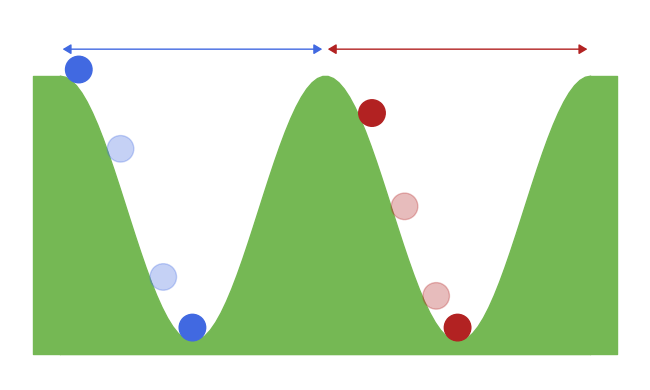
One important characteristic of classical RNNs is the dependency between the new state and the previous one. Given the same input but two different previous states, RNNs can compute two different states. This is the core of their memory. However, this is not that trivial with convergent RNNs. Indeed, the reached state does not always depend on the initial one. For instance, let’s take a valley and a ball that is drop somewhere in that valley. No matter the place where it is dropped (= initial state), it will always end up at the bottom (= reached state). This example is illustrated in figure 2 (left). In other words, no information can be transmitted across updates. Fortunately for us, there is a special property of dynamical system that can help us, which is multistability.

Multistable Systems

A dynamical system is said multistable when, for the same input, it can converge towards different stable states. The reached stable state therefore depends on the input, but also on the initial state of the system. Our previous example with the ball and the valley can easily be extended to exhibit multistability. If an other valley is added next to the first one, then depending where the place is dropped, it might end up at the bottom of the first or the second valley. In this case, there is a dependency between where the ball is dropped, and where it stops. This example is illustrated in figure 2 (right).

Memory Recurrent Units

Memory Recurrent Units (MRUs) are a new type of RNNs build upon this idea of convergent RNNs where the underlying dynamical systems are multistable. MRUs implement true persistent memory, which implies that they can retain any information for an infinite duration. From this concept, we introduce a concrete example, the bistable MRU (BMRU). BMRU is parallelisable like SSMs and can be trained like any classical RNNs. We show that its unique properties bring better memorisation capabilities on several benchmarks. We also show that BMRUs and SSMs can be combined to create hybrid RNNs, where both fading and persistent memory are present, while still being compatible with the parallel scan.

This work has been the subject of a patent application.

References

De Geeter, F., Lambrechts, G., Ernst, D., & Drion, G. (2026). Parallelizable memory recurrent units (No. arXiv:2601.09495). arXiv. https://doi.org/10.48550/arXiv.2601.09495

Gu, A., Goel, K., & Re, C. (2021). Efficiently Modeling Long Sequences with Structured State Spaces. ArXiv. https://www.semanticscholar.org/paper/Efficiently-Modeling-Long-Sequences-with-Structured-Gu-Goel/ac2618b2ce5cdcf86f9371bcca98bc5e37e46f51

Lambrechts, G., De Geeter, F., Vecoven, N., Ernst, D., & Drion, G. (2023). Warming up recurrent neural networks to maximise reachable multistability greatly improves learning. Neural Networks, 166, 645–669. https://doi.org/10.1016/j.neunet.2023.07.023

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., & Polosukhin, I. (2017). Attention is All you Need. Advances in Neural Information Processing Systems, 30. https://proceedings.neurips.cc/paper/2017/hash/3f5ee243547dee91fbd053c1c4a845aa-Abstract.html

Vecoven, N., Ernst, D., & Drion, G. (2021). A bio-inspired bistable recurrent cell allows for long-lasting memory. PLOS ONE, 16(6), e0252676. https://doi.org/10.1371/journal.pone.0252676